Question

A rectangle has a length of (3.2a 1 0.18b) centimeters. The width is half the length. Sasha writes the expression (12.8a 1 0.72b) to represent the perimeter of the rectangle in centimeters. Is Sasha’s reasoning correct? Explain.

Answer 1

No, her reasoning is incorrect.

Explanation:

Given,

The length of the rectangle,

`l = ( 3.2a + 0.18b ) \text{ cm}`,

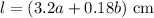Here, the width is half the length.

⇒ Width of the rectangle,

`w = (l)/(2)=(1)/(2)(3.2a + 0.18b)=(3.2a)/(2)+(0.18b)/(2) = (1.6a + 0.09b)\text{ cm}`

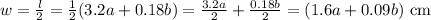
We know that,

The perimeter of a rectangle is,

`P=2(l+w)`

`=2(3.2a + 0.18b+1.6a + 0.09b)`

`=2(4.8a+0.27b)`

`=(9.6a+0.54b)\text{ cm}`

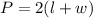
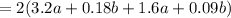
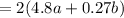
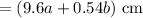
Since, 9.6a + 0.54b ≠ 12.8a + 0.72b

Hence, her reasoning is incorrect.

Answer 2

Perimeter of the rectangle will be given by:
P=2(L+W)
L=(3.2a 10.18b)
W=1/2(3.2a 10.18b)=(1.6a 5.9b)
Thus the perimeter will be:
P=2(3.2a 10.18b+1.6a 5.9b)
P=2(4.8a 16.08b)
P=(9.6a+ 32.16b)

Sasha was not correct