Question

Determine whether each table below models a linear, quadratic or exponential function.

x|y
5|4
6|1
7 |-2
8|-5

x|y
5|0
6|1
7|4
8|8

Answer 1

The correct answers are:

The first table is linear.
The second table is exponential.

Step-by-step explanation:

To see if a set of data is linear, we find the slope. Slope is given by the formula


`m=(y_2-y_1)/(x_2-x_1)`.

We check each pair of points in the first table. The slope between the first two points is:

`m=(1-4)/(6-5)=(-3)/(1)=-3.`

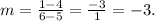
The slope between the second two points is:

`m=(-2-1)/(7-6)=(-3)/(1)=-3`

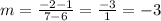
The slope between the third two points is:

`m=(-5--2)/(8-7)=(-5+2)/(8-7)=(-3)/(1)=-3`

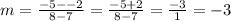
Since the slope is the same between any two pairs of points, this is a linear set of data.

Checking each pair of points in the second table, we have:

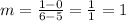
`m=(1-0)/(6-5)=(1)/(1)=1` for the first two points.

For the second pair of points, we have:

`m=(4-1)/(7-6)=(3)/(1)=3`

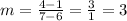
Since the slope is not the same between each pair of points, we know the data is not linear.

Next we will check the second table to see if it is quadratic. Since the x-coordinates go up the same number each time, we can check the y-coordinates, specifically looking at the second differences.

For the second differences, we first find the difference between each y-value:
1-0=1
4-1=3
8-4=4

Now we find the difference between each first difference:
3-1=2
4-3=1

Since these second differences are not the same, the data is not quadratic.

From graphing the data in the table, we can see that the data in the second table is exponential.