Question

An airline has 82% of its flights depart on schedule. It has 65% of its flights depart and arrive on schedule. Find the probability that a flight that departs on schedule also arrives on schedule. Round the decimal to two places.

Answer 1

6.5 out of every 10 flights 65 out of every 100 flights ratio of 6.5 to 10

Answer 2

This question is a case of conditional probability and thus it can be solved by the use of the formula:

`P(B|A)=(P(A\cap B))/(P(A))`

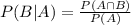
Now, in our case, let A be the event that a flight departs on schedule and let B be the event that a flight arrives on schedule.

Thus, from the given data, we know that:
`P(A) = 0.82` and
`P(A \cap B) = 0.65`

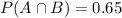
Thus, the conditional probability that a flight that departs on schedule also arrives on schedule will be:

`P(B | A) =( P(B \cap A))/(P(A))=(0.65)/(0.82)\approx0.7927`

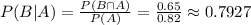
Therefore, when expressed as a percentage, rounded to two places of decimal, the required probability is 79.27%.