Answer:
The mean is the same for both classes
Explanation:
Class A scores of 10 students: 100,100,100,90,95,85,92,98,92,88
Arrange the data in ascending order
85,88,90,92,92,95,98,100,100,100
Mode = 100 since it occurred more times.
Range = Maximum - Minimum = 100-85 = 15
Mean =
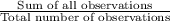
Mean =
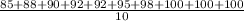
Mean = 94
Median = mid value
n = 10 (even)
So, median =
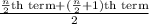
=
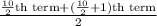
=

=
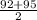
=
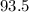
Median = 93.5
Class B scores of 10 students : 100,100,98,95,95,96,95,92,81,88
Arrange the data in ascending order
81,88,92,95,95,95,96,98,100,100
Mode = 95 since it occurred more times.
Range = Maximum - Minimum = 100-81 = 19
Mean =
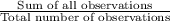
Mean =
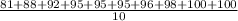
Mean = 94
Median = mid value
n = 10 (even)
So, median =
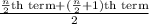
=
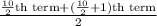
=

=
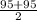
=
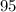
Median = 95
So, The mean is the same for both classes is same i.e. 94.
Hence Option C is correct.