Question

Only answer if you are 100% sure

Answer 1

The answer is: " 2y + 3 " .
____________________________________________________
The quotient is: " 2y + 3 " .
____________________________________________________

Step-by-step explanation:
_____________________________________________
(y − 5) * ( ? ) = 2y² − 7y − 15 ;

_____________________________________________
Solve for " ( ? ) " ;
_____________________________________________

Let us examine:


" 2y² / y = 2y "

_______________________________________________
So: (y − 5) * (2y² ... ? ... ) = 2y² − 7y − 15 ;

Examine the: " -7y " ; and the "-15" ;
____________________________________________________
Factors of: " - 15" ; that add up to "-7" ;
____________________________________________________
Note: the "2" in the "2y² " ; Think of the factors of "±15" ;
(15, 1, 5, 3)

We have "15 and 1" are out;
so "5 and 3" are the options;
we have a "5" (that is, a "-5") in "divisor).

Note the: "-15" ; and we have a "given divisor" containing "-5".

Note: " (-5)" * ( what?) = "(-15)" ? The answer is: " (-15) ÷ (-5) = (3).

The answer is: "3" ; {that is; "positive 3" . }.

Try: (y − 5) * (2y + 3) = ?

Note: (a + b) (c + d) = ac + ad + bc + bd ;


→ (y − 5) * (2y + 3) = (y * 2y) + (y * 3) + (-5 * 2y) + (-5 * 3) ;

= 2y² + 3y + (-10y) + (-15) ;

= 2y² + 3y − 10y − 15 ;

→ Combine the "like terms" ; as follows:
____________________________________________________
+ 3y − 10y = − 7y² ;
____________________________________________________
→ And rewrite the expression:

= 2y² − 7y² − 15 ;
____________________________________________________
So: " (y − 5) * (2y + 3) = 2y² − 7y − 15 " .
____________________________________________________
The answer is: " 2y + 3 " .
____________________________________________________
The quotient is: " 2y + 3 " .
____________________________________________________


Now, suppose we had tried: "(2y − 3)" ; first:
____________________________________________________

→ " (y − 5) (2y − 3) " = ? ;


Note: (a + b) (c + d) = ac + ad + bc + bd ;

→ " (y − 5) (2y − 3) = (y * 2y) + (y * -3) + (-5*2y) + (-5 * -3) ;

= ( 2y² ) + ( -3y ) + ( -10y ) + (15) ;

= 2y² − 3y − 10y + 15 ;

→ Combine the "like terms" ; as follows:

− 3y − 10y = − 13y ;
_____________________________________________________
And we would rewrite the expression as:

= " 2y² − 13y + 15 " ; which means that "this answer" is INCORRECT ; since:
_____________________________________________________
" 2y² − 13y + 15 "
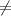`\\eq` " 2y² − 7y − 15 " ;
_____________________________________________________
→ and as such: " 2x − 3"; is NOT the "quotient" — and is NOT the correct answer.
____________________________________________________

Answer 2

`\frac{2 {y}^(2) - 7y - 15 }{y - 5} = 2y \\ remainder \: \frac{2 {y}^(2) - 7y - 15 }{ - (2{y }^(2) - 10y + 0)} \\ = 3y - 15`

`(3y - 15)/(y - 5) = 3 \\ remainder \: (3y - 15)/( - (3y - 15)) = 0`
So the quotient is : 2y + 3, with no remainder