Question

VERY IMPORTANT! PLEASE ANSWER FULLY

Jeremy and Arnold were thinking about their recent math lessons on the volume of a cylinder and the volume of a cone. They were curious to see how many cones it would take to fill a cylinder. “Let’s just make the shapes and see for ourselves,” suggested Jeremy. While Arnold thought it was a good idea, he and Jeremy struggled to construct the shapes so that the radius and heights of each figure were the same. Will you help them in their investigation? (If you don’t want to use the shapes they provided, you can use any can or cone but they have to be the same height and have the same diameter)
Part I: Construction Nets for a cone and a cylinder are provided. Cut out each shape and secure the edges with a piece of tape.

Part II: Filling the Shapes Fill the cone with a dry ingredient like rice or beans. Pour the contents of the cone into the cylinder. Repeat this process until the cylinder is full.

How many cones does it take to fill the cylinder?




Write the formulas for the volume of each shape.


Vcyl = _______________ Vcone = _______________



Explain the relationship between the volume of the cylinder and the volume of the cone.

Answer 1

volume of cylinder= π•r•r•h
volume of cone= π•r•r•h
---------
3

it takes 3 cones to fill a cylinder if bot shape have an equal base and equal height.

Answer 2

3 cones are required to fill the cylinder.

Vcyl =
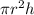`\pi r^2 h` and Vcone =
`(1)/(3) \pi r^2 h`

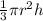
The volume of cylinder is 3 times the volume of cone having same base and height.

Explanation:

Consider the provided information.

Now we need to find the number cones to fill the cylinder.

The volume of a cone is:

`(1)/(3) \pi r^2 h`

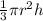
The volume of cylinder is:

`\pi r^2 h`

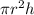
To find the the number cones to fill the cylinder simply divide the volume of cylinder by volume of cone as shown:

`(\pi r^2 h)/((1)/(3) \pi r^2 h)=3`

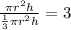
Hence 3 cones are required to fill the cylinder.

The formula for the volume of each shape is:

Vcyl =
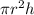`\pi r^2 h` and Vcone =
`(1)/(3) \pi r^2 h`

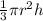
The relationship between the volume of the cylinder and the volume of the cone is: The volume of the cone is 1/3 of a cylinder that has the same base and height or the volume of cylinder is 3 times the volume of cone having same base and height.