Question

Write the slope-intercept inequality for the graph below (1,2) (3,-2)

Answer 1

The points given to us are:
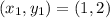`(x_1,y_1)=(1,2)` and
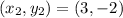`(x_2,y_2)=(3,-2)`. To find the line that passes through these points, we will use the formula:

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

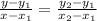
Thus, employing this formula we get:

`(y-2)/(x-1)=(-2-2)/(3-1)=(-4)/(2)=(x)/(y) =-2`

Thus,
`(y-2)/(x-1)=-2`

`y-2=-2(x-1)`

`y=-2x+2+2=-2x+4`

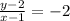
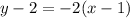
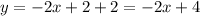
Thus the slope-intercept form of the line passing through the points (1,2) and (3,-2) is:
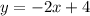`y=-2x+4` and is depicted by the dotted line in the graph attached. Now, since we want the slope-intercept inequality for the graph below the points (1,2) and (3,-2), we will write the inequality as:
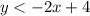`y<-2x+4`. The region that represents the inequality is shown in the graph attached.