Answer:
The difference in the volume of cylinder and total surface area of cylinder =
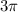 .
.
The number of sq units of total area exceeds the number of cu.units in the volume
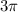 .
.
Explanation:
Given radius of cylinder =1 unit
Height of cylinder= 1 unit
We know that formula of volume of cylinder =
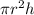
Where r= Radius of the cylinder
h= Height of the cylinder
By using this formula we can find the volume of cylinder
volume of cylinder =
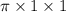 =
=
![\pi cubic units.</p><p>Formula of total surface area of cylinder:</p><p> Total surface area of cylinder = [tex]2\pi r(r+h)](https://img.qammunity.org/2019/formulas/mathematics/college/45cr3bznwz9wsa467p7i7yxuicz9a6mo7n.png)
By using this formula we can find total surface area of cylinder
Total surface area of cylinder =
![2\pi * 1(1+1)[/tex}</p><p> Total surface area of cylinder=[tex]4\pi](https://img.qammunity.org/2019/formulas/mathematics/college/9x94ed24566t5c4t65z2aazpo016636hg6.png) sq units .
sq units .
Difference between volume of cylinder and total surface area of cylinde=
 =
=
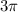
Total surface area of cylinder - volume of cylinder=
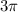
Total surface area of cylinder =
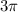 + volume of cylinder
+ volume of cylinder
Hence, the number of sq units of total surface area exceed the number of cu.units in the volume by
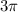 .
.