Let the required balance be
 .
.
Thus, for Card A, which has an APR of 26.2% and an annual fee of $30, the amount after a year when compounded monthly will be:
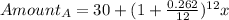 ........(Equation 1)
........(Equation 1)
Likewise, for Card B, which has an APR of 27.1% and no annual fee, the amount after a year when compounded monthly will be:
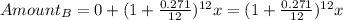 ....(Equation 2)
....(Equation 2)
Therefore, all else being equal, the balance,
 , at which the cards offer the same deal over the course of a year can be found by equating the equations 1 and 2 and solving for x.
, at which the cards offer the same deal over the course of a year can be found by equating the equations 1 and 2 and solving for x.
Thus we have:

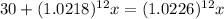
Simplification gives us:
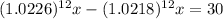
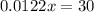
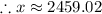 dollars
dollars
This is the closest to the second option. Thus, option B is the correct option.
Important Note: If we do not round off the intermediate steps and calculate it directly using a calculator then we will get the exact answer of option B which is: $2617.85.