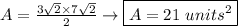We are asked to find two things, namely:
1. The coordinates of the vertices of the triangle.
2. Compute the area of the triangle using the distance formula.Let's solve this exercise step by step, so:1. To do this we will see the the figure below to find out the points of each vertex. Thus, the three points are as follows:
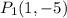
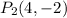
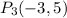
2. The area of a triangle is given by this formula:
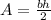
where b is the base and h the height of the triangle. We can use the Distance Formula to solve this problem so:
![b=\overline{P_(1)P_(2)}=\sqrt{(x_(1)-x_(2))^2+(y_(1)-y_(2))^2} \\ \therefore b=√((1-4)^2+[-5-(-2)]^2)=3√(2)](https://img.qammunity.org/2019/formulas/mathematics/college/2lblardjiv8zu49w67a1y9dkmufvu0dgxk.png)
![h=\overline{P_(2)P_(3)}=\sqrt{(x_(2)-x_(3))^2+(y_(2)-y_(3))^2} \\ \therefore b=√([4-(-3)]^2+(-2-5)^2)=3√(2)=7√(2)](https://img.qammunity.org/2019/formulas/mathematics/college/4yymzzlgf4irw3lsebdr4b7xs084fyfdx9.png)
Finally the area is: