Question

A set of data has a mean of 56.1. The data follows a normal distribution curve and has a standard deviation of 8.2. Find the probability that a randomly selected value is greater than 67.5

A.
0.0823

B.
1.39

C.
0.9177

D.
–1.08

Answer 1

Answer: A. 0.0823

Explanation:

Given : Mean
`\mu`=56.1

Standard deviation
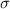`\sigma`=8.2

P(x>67.5) will be found as follows:

The z-score is given by:

`z=(X-\mu)/(\sigma)`

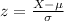
Substitute the values of means ans standard deviation in it, we get

`\Rightarrow\ z=(67.5-56.1)/(8.2)\\\\\Rightarrow\ z=(11.4)/(8.2)\\\Rightarrow\ z=1.39`

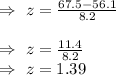
As

P(z<1.39)=0.9177

thus:

P(X>67.5)=1-P(z<1.39)

⇒P(X>67.5)=1-0.9177

∴P(X>67.5)=0.0823

Answer 2

Given that mean=56.1 and standard deviation=8.2, P(x>67.5) will be found as follows:
The z-score is given by:
z=(x-μ)/σ
thus the z-score will be given by:
z=(67.5-56.1)/8.2
z=11.4/8.2
z=1.39
thus
P(z=1.39)=0.9177
thus:
P(x>67.5)=1-P(z>0.9177)
=1-0.9177
=0.0823
Answer: A. 0.0823