Question

Which sequence is modeled by the graph below? points are (1,3) (2,0.6) (3, 0.12)

A an = 3 (one fifth )^n − 1
B an = 3(−5)^n − 1
C an = 0.3(5)^n − 1
D an = one fifth (3)^n − 1

Answer 1

ANSWER

`a_n =3( (1)/(5) ) ^(n - 1)`
Explanation

The ordered points given to us are

`(1,3),(2,0.6),(3,0.12)`
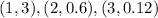
The y-coordinates are the terms in the sequence.

We use the y-coordinates to determine the common ratio.


`r = (0.6)/(3) = (0.12)/(0.6) = (1)/(5)`

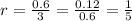
The first term of the sequence is the first y-coordinate.


`a_1 = 3`

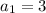
The nth term of an exponential sequence is given by,




`a_n =a_1 * r ^(n - 1)`


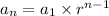
We now substitute the above values in to the general formula to obtain,



`a_n =3( (1)/(5) ) ^(n - 1)`