Question

Question 1 Gary is on the space shuttle. It takes off and lifts him to a height of 300 km above Earth's surface. a. How has Gary's mass changed? Explain. b. How has Gary's weight changed? Explain.

Answer 1

a) The mass is an intrinsic property of an object: it means it depends only on the properties of the object, so it does not depend on the location of the object. Therefore, Gary's mass at 300 km above Earth's surface is equal to his mass at the Earth's surface.

b) The weight of an object is given by

`W=mg`
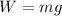
where
m is the mass

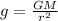
`g= (GM)/(r^2)` is the gravitational acceleration at the location of the object, with G being the gravitational constant, M the mass of the planet and r the distance of the object from the center of the planet.

At the Earth's surface,
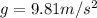
`g=9.81 m/s^2`, so Gary's weight is

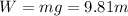
`W=mg=9.81 m` (1)
where m is Gary's mass.

Then, we must calculate the value of g at 300 km above Earth's surface. the Earth's radius is

`R=6370 km`
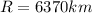
So the distance of Gary from the Earth's center is

`r=R+h=6370 km+300 km =6670 km = 6.67 \cdot 10^6 m`

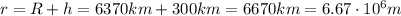
The Earth's mass is
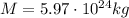
`M=5.97 \cdot 10^(24) kg`, so the gravitational acceleration is

`g'=G (M)/(r^2)= (6.67 \cdot 10^(-11) m^3 kg^(-1) s^(-2) )(5.97 \cdot 10^(24) kg)/((6.67 \cdot 10^6 m)^2)=8.95 m/s^2`

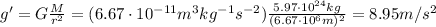
Therefore, Gary's weight at 300 km above Earth's surface is

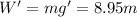
`W' = mg' = 8.95 m` (2)

If we compare (1) and (2), we find that Gary's weight has changed by

`(W')/(W)= (8.95 m)/(9.81 m)=0.91`
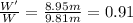
So, Gary's weight at 300 km above Earth's surface is 91% of his weight at the surface.