Answer:

OR
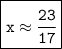
Explanation:
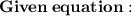
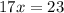
Make x the subject means we need to find the value of x.

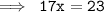
Divide each side by 17 :
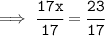
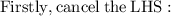
- Cancel 17 ( which is on the numerator ) and cancel 17 ( which is on the denominator ) :-
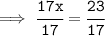
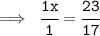
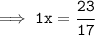


But, We can convert 23/17 into decimal form.
That is,

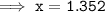
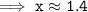
Hence, the value of x would be 23/17 or 1.4 .

I hope this helps!
Let me know if you have any questions.
:D