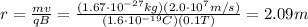Question

a proton moves at a speed of 2.0 x 10^7 m/s at right angles to a magnetic field that is directed into the page with a magnitude of 0.1T, Calculate the radius of the orbit

Answer 1

The Lorentz force acting on the proton is equal to:

`F=qvB \sin \theta`
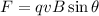
where
q is the proton charge
v is the proton speed
B is the intensity of the magnetic field

`\theta` is the angle between the direction of v and B

since the proton travels perpendicularly to the magnetic field, in this case
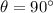
`\theta=90^(\circ)`, so the Lorentz force in this case is simply

`F=qvB`

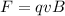
The magnetic force provides also the centripetal force that keeps the proton in circular motion:

`m (v^2)/(r)=qvB`
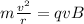
where
m is the proton mas
r is the radius of the orbit

If we re-arrange this equation and we use the data of the problem, we can find the radius of the orbit:

`r= (mv)/(qB)= ((1.67 \cdot 10^(-27) kg)(2.0 \cdot 10^7 m/s))/((1.6 \cdot 10^(-19) C)(0.1 T)) =2.09 m`