Question

What speed must an electron have if its momentum is to be the same as that of an x-ray photon with a wavelength of 0.20 nm?

Answer 1

The momentum of a photon is given by the following relationship:

`p= (h)/(\lambda)`
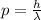
where
h is the Planck constant

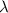
`\lambda` is the photon wavelength

For the photon in our problem,
`\lambda=0.20 nm = 0.20 \cdot 10^(-9)m`, so its momentum is

`p= (h)/(\lambda)= (6.6 \cdot 10^(-34) Js)/(0.20 \cdot 10^(-9) m)=3.3 \cdot 10^(-24) kg m/s`

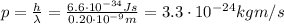
The electron must have the same momentum of this photon, and its momentum is given by (in the non-relativistic approximation)

`p=mv`
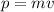
where
m is the electron mass
v is its speed

Re-arranging this formula, we can calculate the electron speed:

`v= (p)/(m)= (3.3 \cdot 10^(-24) kg m/s)/(9.1 \cdot 10^(-31) kg) =3.6 \cdot 10^6 m/s`

And this velocity is quite small compared to the speed of light (
`c=3 \cdot 10^8 m/s`), so the non-relativistic approximation that we used for the electron's momentum is valid.