The distance covered by car is equal to (assuming it is moving by uniform motion) the product between the car's speed and the time of the car ride, 4 h:
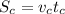
where
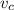
is the car's speed

is the duration of the car ride
Similarly, the distance covered by train is equal to the product between the train's speed and the duration of the train ride, 7 h:
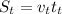
The total distance covered is S=255 km, which is the sum of the distances covered by car and train:
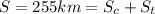
which becomes
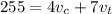
(1)
we also know that the train speed is 5 km/h greater than the car's speed:
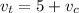
(2)
If we put (2) into (1), we find
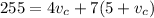
and if we solve it, we find
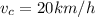
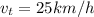
So, the car speed is 20 km/h and the train speed is 25 km/h.