Question

An object has a weight of 100 N on the surface of the Earth. If the object is moved to 2RE above the surface of the Earth, its weight is

25.0 N.

11.0 N.

0 N.

100 N.

Answer 1

Weight of the object is defined as

`W = mg`

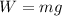
here

m = mass of object

g = acceleration due to gravity

now at the surface of earth

`g = (GM)/(R_e^2)`

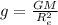
so given that

`mg = 100 N`

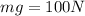
now when it is moved to distance 2Re from the surface so its distance from the center of earth will be given as Re + 2Re = 3Re

so acceleration due to gravity will be given as

`g' = (GM)/((3R_e)^2) = (GM)/(9R_e^2)`

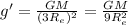
so now weight is given as

`W = m*(g)/(9)`

`W = (100)/(9) = 11.1 N`

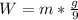
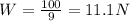
so now weight will be 11 N