Answer:
The steps are at –2 from 0 to 1, at –1 from 1 to 2, and at 0 from 2 to 3.
A is correct
Explanation:
Given: f(x)=[x]-2 on [0,3)
It is greatest integer function.
Parent function: f(x)=[x]
Graph shift 2 unit down.
f(x)=[x]-2
Now we make table
x : 0 0.5 1 1.5 2 2.5 <3
f(x) : -2 -2 -1 -1 0 0 0
From table
f(x)=-2 on [0,1)
f(x)=-1 on [1,2)
f(x)=0 on [2,3)
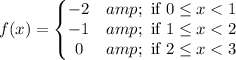
Hence, The steps are at –2 from 0 to 1, at –1 from 1 to 2, and at 0 from 2 to 3.