Question

What is the measure of ∠F, to the nearest degree?

44°

57°

71°

78°

Answer 1

A.
`44^(\circ)`

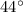
Explanation:

We have been given a triangle FGH, we are asked to find the measure of angle F.

We will use law of cosines to solve our given problem.

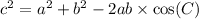`c^2=a^2+b^2-2ab* \text{cos}(C)`, where, a, b and c are sides of triangle and C is the angle opposite to side c.

Upon substituting our given values in above formula we will get,

`5^2=7^2+6^2-2*7*6* \text{cos}(F)`

`25=49+36-84* \text{cos}(F)`

`25=85-84* \text{cos}(F)`

`25-85=85-85-84* \text{cos}(F)`

`-60=-84* \text{cos}(F)`

`(-60)/(-84)=\frac{-84* \text{cos}(F)}{-84}`

`(5)/(7)=\text{cos}(F)`

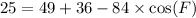
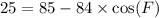
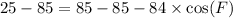
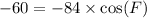
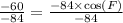
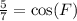
Now we will use arccos to solve for measure of angle F.

`F=\text{cos}^(-1)((5)/(7))`

`F=44.415308597^(\circ)\approx 44^(\circ)`

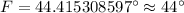
Therefore, the measure of angle F is 44 degrees and option A is the correct choice.

Answer 2

Three lines given -- it's a natural for the cos(theta) law. A small hint: I think the preferred way of doing it is to use the cos(theta) law twice. It will give you a definite answer.

Find G first
g = 6 yd
h = 7 yd
f = 5 yards.

g^2 = h^2 + f^2 - 2*h*f*cos(G)
6^2 = 7^2 + 5^2- 2*7*5*cos(G)
36 = 49 + 25 - 70*Cos(G)
36 = 74 - 70*cos(G)
-48 = - 70 * cos(G) Divide by -70
-38/-70 = cos(G)
0.5429 = cos(G)
cos-1(0.5429) = G
G = 57.12

Now find H
h^2 = g^2 + f^2 - 2*g*f*cos(H)
7^2 = 5^2 + 6^2 - 2*5*6*cos(H)
49 = 25 + 36 - 60cos(H)
49 =61 - 60*cos(H)
Cos(H) = -12 / - 60
Cos(H) = 0.2
H = cos-1(0.2)
H = 78.46

F can be found because every triangle has 180 degrees
F + 78.46 + 57.12 = 180
F + 135.58 = 180
F = 180 - 135.58
F = 44.41

A <<<< Answer.