Question

Tom throws a ball into the air. The ball travels on a parabolic path represented by the equation h = 08t^2 + 40t, where h represents the height of the ball above the ground and t represents the time in seconds.

How many seconds does it take the ball to reach its highest point?

What ordered pair represents the highest point that the ball reaches as it travels through the air?

Answer 1

It takes 1.25 seconds to reach the highest point, and that is given by the ordered pair (1.25, 37.5).

To find the highest point, we find the axis of symmetry first. This is given by
-b/2a:
-40/2(-16) = 40/32 = 1.25.

Now we plug this into the function:
-8t²+40t = -8(1.25)²+40(1.25) = -12.5 + 50 = 37.5.

Answer 2

A quadratic equation is of the form
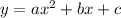`y=ax^2+bx+c` ...[1] then the axis of symmetry is given by:

`x = -(b)/(2a)`

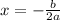
As per the statement:

The ball travels on a parabolic path represented by the equation is:

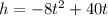`h= -8t^2+40t` ....[2]

where,

h represents the height of the ball above the ground

t represents the time in seconds.

To find how many seconds does it take the ball to reach its highest point.

On comparing with [1] we have;

a = -8 and b = 40

then:

axis of symmetry is :

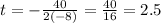`t =-(40)/(2(-8)) = (40)/(16) = 2.5` sec

⇒2.5 seconds does it take the ball to reach its highest point.

Substitute the value of t =2.5 sec in [2] we have;

`h = -8(2.5)^2+40(2.5) = -50+100 = 50`

Ordered pair = (2.5, 50)

Therefore, (2.5, 50) ordered pair represents the highest point that the ball reaches as it travels through the air