Question

The u.s. department of health and human services collected sample data for 772 males between the ages of 18 and 24. that sample group has a mean height of 69.7 inches with a standard deviation of 2.8 inches. find the 99% confidence interval for the mean height of all males between the ages of 18 and 24.

Answer 1

Answer: (69.44, 69.96).

Explanation:

Given : Sample size : n= 772

Significance level :
`\alpha: 1-0.99=0.01`

Critical value :
`z_(\alpha/2)=\pm2.576`

Sample mean :
`\overline{x}=69.7`

Standard deviation:
`\sigma=2.8`

The confidence interval for population mean is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))`

i.e
`69.7\pm(2.576)(2.8)/(√(772))`

i.e
`\approx69.7\pm0.26=(69.7-0.26,\ 69.7+0.26)=(69.44,\ 69.96)`

Hence, the confidence interval for the mean height ( in inches) of all males between the ages of 18 and 24 is (69.44 , 69.96).

Answer 2

The 99% confidence interval for the true mean is given by:


`\bar{x}\pm z_(\alpha/2) (\sigma)/(√(n))`

where:


`\bar{x}` is the sample mean = 69.7

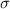
`\sigma` is the standard deviation = 2.8

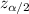
`z_(\alpha/2)` is the test statistics = 2.58 for for 99% confidentce interval.
n is the sample size = 772.

Therefore, the 99% confidence interval is:


`69.7\pm2.58\left( (2.8)/(√(772)) \right)=69.7\pm2.58(0.1008) \\ \\ =69.7-0.26\leq\mu\leq69.7+0.26 \\ \\ =69.44\leq\mu\leq69.96`