Question

A 40 cm. diameter sphere that weighs 400 n is released from rest underwater in claytor lake. its initial acceleration is about:

Answer 1

Newton's second law states that the resultant of the forces acting on the sphere is equal to the product between its mass m and its acceleration a:

`\sum F = ma`

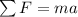
There are two forces acting on the sphere: its weight W, directed downward, and the buoyancy B, directed upward. So Newton's second law becomes

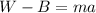
`W-B = ma` (1)

We already know the weight of the sphere:
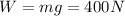
`W=mg=400 N`, from which we can also find the mass of the sphere:

`m= (W)/(g)= (400 N)/(9.81 m/s^2)=40.8 kg`

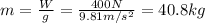
The buoyancy is equal to the mass of the water displaced:

`B=\rho_W V g`
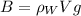
where

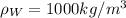
`\rho_W = 1000 kg/m^3` is the water density
V is the volume of water displaced, which corresponds to the volume of the sphere, since the sphere is underwater
g is the gravitational acceleration
The radius of the sphere is

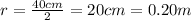
`r= (40 cm)/(2)=20 cm=0.20 m`, so its volume is

`V= (4)/(3) \pi r^3 = (4)/(3)\pi (0.20 m)^3 = 3.55 \cdot 10^(-2) m^3`

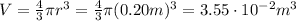
So now we can rewrite Newton's second law (1) as

`mg-\rho_W V g = ma`
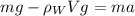
and solve it to find the acceleration of the sphere, a:

`a=g- (\rho_W V g)/(m)=9.81 m/s^2 - ((1000 kg/m^3)(3.55 \cdot 10^(-2) m^3)(9.81 m/s^2))/(40.8 kg) =1.76 m/s^2`

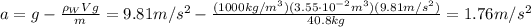
and this acceleration is directed downward, since it has the same sign of g.