Let's call the number x. The square of a number would be

. This is 12 more than the number itself. 12 more than the number is 12+x.
Putting this together we get
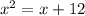
This is a quadratic equation so we set it equal to zero by subtracting x+12 from both sides. We obtain:
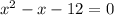
The left-had side factors as such:
(x-4)(x+3)=0
Since we have two expressions that when multiplied give zero either one or both equal zero. We set each equal to zero to obtain the solutions:
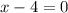
so x =4
and
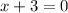
so x=-3
The two solutions are 4 and -3