Question

A line passes through each pair of points. Determine if the system has no solution, one solution, or an infinite number of solutions.

(4,1) and (0,1)
(0,-4) and (4,4)

Answer 1

Let's take each pair of points and find the slope of the line that connects them.

For each pair of points let's call the first one
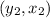
`( y_(2) , x_(2) )` and the second
`( y_(1) , x_(1) )`.

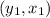
We then substitute into the formula for the slope which is:

`m= ( y_(2) - y_(1) )/( x_(2) - x_(1) )`

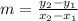
FIRST PAIR OF POINTS

`m= (1-1)/( 4-0)=0`

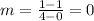
SECOND PAIR OF POINTS

`m= (-4-4 )/( 0-4)=2`

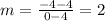
If two line have the same slope they are parallel and do not meet. These have different slopes so they are not parallel and will intersect at a point. That point gives the one solution to the system.

The system has one solution.