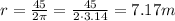The length of the fencing corresponds to the length of the perimeter of the garden:

We also know that the perimeter of a circle is given by:

where r is the radius of the circle.
Putting together the two equations, we have
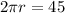
from which we can find r, the radius of the garden: