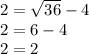Question

Find two numbers if the second number equals 4 less than the square of the first number and their sum is 38.

Answer 1

36 divided by 6 is 6
2 is 4 less than 6
3 and. 36 make. 38

Answer 2

We can set up a system of equations like this, where x is the first number and y is the second:


`\left \{ {{y= √(x) -4} \atop {x+y=38}} \right`

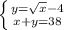
Since we know what y is equal to, we can plug that into the second equation for y to solve for x:


`\\ x+ √(x) -4=38 \\ x+ √(x) -42 =0 \\ √(x) = 42-x \\ (√(x))^(2) = (42-x)^(2) \\ x = 1764 - 84x + x^(2) \\ x^(2) -85x+1764 = 0 \\ (x-36)(x-49)=0 \\ x = 36, 49`

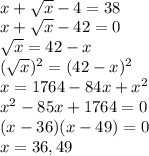
x can equal either 36 or 49. If x equals 36:


`36+y=38 \\ y=2`

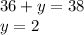
If x equals 49:


`49+y = 38 \\ y = -11`

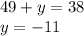
Although both are solutions, x=36 and y=2 or x=49 and y=-11, I would use x=36 and y=2 because plugging the 49 and -11 in causes a predicament:


`-11 = √(49)-4 \\ -11=7-4 \\ -11 \\eq 3`

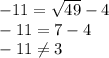
*Note that the negative solution of √49 does work

Plugging in 36 and 2 turns out fine:


`2 = √(36) -4 \\ 2 = 6-4 \\ 2 = 2`