Answer:
Option C is correct.
The probability of maximum distance between 125 and 135 miles is , 0.5531
Explanation:
Let X be the distance traveled by car between 125 and 135 miles.
Also, given: The mean distance(
 ) = 134 miles and the standard deviation(
) = 134 miles and the standard deviation(
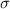 ) = 4.8 miles.
) = 4.8 miles.
To calculate the Probability that in a random test rum the car will travel a maximum distance between 125 and 135 miles i.e:
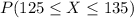
Let
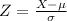
then the corresponding z-values need to be computed are:

and

Therefore, the following is obtained:
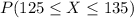 =
=
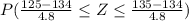 =
=
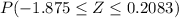
=

Now, using Standard Normal distribution table we have:
= 0.5835 - 0.0304=0.5531
Therefore, the probability that in a random test run the car will travel a maximum distance between 125 and 135 miles is, 0.5531.