Given a complex number in the form:
![z= \rho [\cos \theta + i \sin \theta]](https://img.qammunity.org/2019/formulas/mathematics/high-school/labn0rdry6bszagbluhc8z372j8un1hcud.png)
The nth-power of this number,
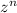
, can be calculated as follows:
- the modulus of
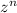
is equal to the nth-power of the modulus of z, while the angle of
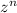
is equal to n multiplied the angle of z, so:
![z^n = \rho^n [\cos n\theta + i \sin n\theta ]](https://img.qammunity.org/2019/formulas/mathematics/high-school/cldi4n20p7aerrmq9nloqahkms8o46s7hv.png)
In our case, n=3, so
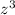
is equal to
![z^3 = \rho^3 [\cos 3 \theta + i \sin 3 \theta ] = (5^3) [\cos (3 \cdot 330^(\circ)) + i \sin (3 \cdot 330^(\circ)) ]](https://img.qammunity.org/2019/formulas/mathematics/high-school/iiwcfk3rxy1tc00ir0j7hh4pptfgntz454.png)
(1)
And since
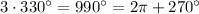
and both sine and cosine are periodic in
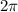
, (1) becomes
![z^3 = 125 [\cos 270^(\circ) + i \sin 270^(\circ) ]](https://img.qammunity.org/2019/formulas/mathematics/high-school/g5s735dbmiufgc5x7gx2588m42qqfm9vs1.png)