Question

Which of the following is the complete list of roots for the polynomial function f(x) = (x2 + 2x - 15)(x2 + 8x + 17)?

A) -5,3
B) -5,3,-4,+I,-4,-i
C) -5,3,-4,+I,4+I
D) -4+i , -4 -i

Answer 1

The first one factors easily. The first quadratic, I mean. The 2 numbers that add up to +2 and at the same time multiply to -15 and 5 and -3. So those are 2 of the 4 roots we have. The second quadratic does not factor so nicely. You need to put that into the quadratic formula to solve.
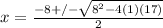
`x= (-8+/- √(8^2-4(1)(17)) )/(2)` which simplifies to
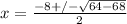
`x= (-8+/- √(64-68) )/(2)`. That gives us a negative radicand and that's a problem.
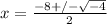
`x= (-8+/- √(-4) )/(2)`. Since -1 is equal to i^2, we can rewrite to begin dealing with the negative properly.
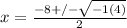
`x= (-8+/- √(-1(4)) )/(2)`. Replacing -1 with i^2 gives us
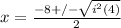
`x= (-8+/- √(i^2(4)) )/(2)`. i^2 has a perfect root of i in it, and 4 has a perfect square of 2 in it, so we simplify more to
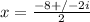
`x= (-8+/-2i)/(2)`. The 2 in the denominator reduces with the numerator to give us a final 2 roots that are x = -4 + i, and x = -4 - i. Taking all those roots together, we find that the solution to our problem is choice B (although I believe you put some extra commas in there on accident).

Answer 2

Given polynomial function f(x) = (x^2 + 2x - 15)(x^2 + 8x + 17).

In order to find all roots of the given polynomial function, we need to set each of above factor equal to 0.

Therefore,

x^2 + 2x - 15 =0 and x^2 + 8x + 17 =0.

Let us solve first quadratic now.

x^2 + 2x - 15 =0

Factoring out quadratic

(x+5)(x-3) =0

x+5=0 or x-3=0

x=-5 or x=3.

Let us solve second quadratic equation now

x^2 + 8x + 17 =0.

Applying quadratic formula,

`\quad x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`x_(1,\:2)=(-8\pm √(8^2-4\cdot \:1\cdot \:17))/(2\cdot \:1)`

`x=(-8+√(8^2-4\cdot \:1\cdot \:17))/(2\cdot \:1):\quad -4+i`

`x=(-8-√(8^2-4\cdot \:1\cdot \:17))/(2\cdot \:1):\quad -4-i\`

`x=-4+i,\:x=-4-i`

Therefore, the list of roots for the polynomial function is:

`x=3,\:x=-5,\:x=-4+i,\:x=-4-i.`

So, the correct option is B) -5, 3, -4+i, -4-i.