Question

For the equation x2 = a, describe the values of a that will result in two real solutions, one real solution, and no real solution. complete the explanation below.

Answer 1

The equation given is
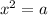
`x^(2) =a` where a is some number.
We can solve for x by taking the square root of both sides.


`x=plusminus √(a)`

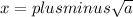
Now let's think through what happens for various values of a.

TWO SOLUTIONS
If a is a positive number the above yields two solutions. Take for example:

`x^(2) =49 √(49)=7 or -7`
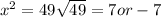
There will be two solutions (one positive and one negative) as there are two numbers (here -7 and +7) that when multiplied by themselves give 49. That is,
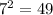
`7^(2) =49` and
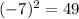
`(-7)^(2)=49`. The positive root is called the principal root and the negative root is called the secondary root. This will be the case anytime we take the root of a positive number.

ONE SOLUTION
If a = 0 there is only one solution. That is because
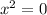
`x^(2) =0` and
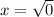
`x= √(0)`. Zero is neither positive nor negative and it has only one root which is 0 itself. So in this case there is only one solution and it is 0.

NO (REAL) SOLUTIONS
If a is negative we would be taking the square root of a negative number. There is no (real) number that when multiplied by itself gives a negative number. Take for example
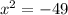
`x^(2) =-49` which gives us
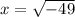
`x= √(-49)`. The square root of -49 is not 7 because (7)(7)=49 which is positive. The square root of -49 is not -7 because (-7)(-7)=49 which is also positive. There is no real number that gives -49 when multiplied by itself. I say "real" numbers because there do exist imaginary/complex numbers but because of the way the questions was asked I imagine you may not know about these yet.