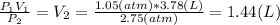Answer:
1.44 L
Step-by-step explanation:
According with Ideal gas law, it can be represented the dependencies between temperature, pressure, volume and molar amount of a ideal gas as follows:
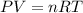
Where:

In this case the gas is contained in a balloon with a initial pressure, volume, molar amount and temperature (
 ) and changes to a second state with a final pressure, volume, molar amount and temperature (
) and changes to a second state with a final pressure, volume, molar amount and temperature (
 ). As we know, R is the Ideal Gas Constant and do not change with the state changes, then it is possible to obtain the equation:
). As we know, R is the Ideal Gas Constant and do not change with the state changes, then it is possible to obtain the equation:

But the state change proceed at constant temperature and molar amount, then
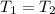 and
and
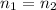 and replacing in the previews equation we obtain:
and replacing in the previews equation we obtain:
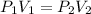
So we can obtain the final Volume as follows: