Note: I assume the altitude is measured from Earth's center (it's not clear from the text if it's from the Earth's center or from the surface)
The force of gravity experienced by the object is given by
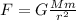
where
G is the gravitational constant
M is the mass of the Earth
m is the mass of the object
r is the distance of the object from Earth's center
Initially, its distance from Earth's center is twice the Earth radius:
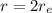
, so the force of gravity is
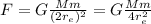
Later, the object altitude is doubled, so its new distance from Earth's center is 4 times the Earth's radius:
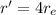
and so the new force of gravity is
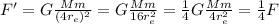
therefore, the new force is 1/4 of the original force.