Question

A circuit consists of a battery connected to three resistors (65 ω, 25ω, and 170ω) in parallel. the total current through the resistors is 1.8

a. find (a) the emf of the battery and (b) the current through each resistor.

Answer 1

Answer: 29.37V

Step-by-step explanation:

1/65 +1/25 + 1/170= 0.06126

Resistance equal= 1/0.06126= 16.32ω

Voltage= (1.8A)(16.32ω)=29.37V

Answer 2

A. To find the total emf of the battery, just remember that in a parallel circuit, the voltage is the same throughout the circuit. So you can get the total voltage of the circuit by using Ohm's Law.


`I= (V)/(R)`

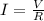
Where:
I = current (A)
V = Voltage (V) (emf)
R = Resitance (Ω)

Now you can derive the formula of Voltage by transposing the Resistance to the other side of the equation to isolate Voltage. The formula you will now use will be:

`V = IR`

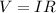
However, you cannot solve this yet because the resistance you need is the total resistance in the circuit. To do this, you need to get the total resistance in this parallel circuit and the formula would be:


`(1)/(R_(T)) = (1)/(R_(1))+ (1)/(R_(2))+ (1)/(R_(3))...+ (1)/(R_(n))`

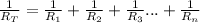
You have three resistors with the following resistance:
65Ω, 25Ω and 170Ω

`(1)/(R_(T)) = (1)/(R_(1))+ (1)/(R_(2))+ (1)/(R_(3))...+ (1)/(R_(n))`


`(1)/(R_(T)) = (1)/(R_(65))+ (1)/(R_(25))+ (1)/(R_(170))`



`(1)/(R_(T)) =0.0153+0.04+0.006+0.0059`

`(1)/(R_(T)) =0.0613`

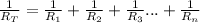
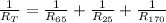
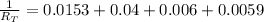
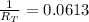
Get the reciprocal of both sides and divide:


`R_(T) = (1)/(0.0613) =16.32`

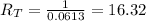The total resistance then is 16.32Ω

Now that you have the total resistance, you can solve for the total voltage:

`V = IR`

`V = (1.8)(16.32)`

`V = 29.376V`

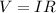
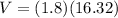
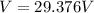
The emf of the battery is 29.376V

B. To find the resistance in each resistor, just apply Ohm's law again. In a parallel circuit, the voltage is the same, but the current that runs through it is different for each resistor. Now just solve for the current of each using the same voltage.

Resistor 1: 65Ω

`I= (V)/(R)`

`I= (29.376)/(65)`

`I= 0.45A`

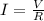
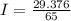
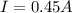
The current flowing through resistor 1 with a resistance of 65Ω is 0.45A.

Resistor 2: 25Ω

`I= (V)/(R)`

`I= (29.376)/(25)`

`I= 1.18A`
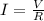
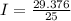
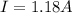
The current flowing through resistor 2 with a resistance of 25Ω is 1.18A.

Resistor 3: 170Ω

`I= (V)/(R)`

`I= (29.376)/(170)`

`I= 0.17A`

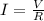
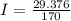
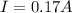
The current flowing through resistor 3 with a resistance of 170Ω is 0.17A.

If you add up all their current it confirms the given that the total current running through all of them is 1.8A.