Answer:
The model that describes the relationship between the amount of money in an account and time, given that the money doubles every month is:
Exponential
Explanation:
Let the initial amount of money be: x
- i.e. amount of money in first month= x
- Hence, if money doubles every month then the amount of money in second month is: 2x
- In third month it will be:
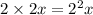
- In fourth month it will be:
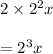
and so on,
Hence, the amount of money in nth month is:
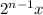
As the amount of money increases by a fixed multiplicative rate i.e. 2.
Hence, the model is:
Exponential.