Question

What is the domain and range of f(x)=(1/6)^x-2

Answer 1

Find the domain by finding where the function is defined. the range is the set of values that correspond with the domain
Domain:(-∞,∞),x∈ R
Range:Y>-2

Answer 2

Explanation:

The given function is a exponential .

There is no restriction on the input values of an exponential , That means there is no restriction on the x whose possible values determines the domain. So the Domain of f(x) is (-∞,∞).

Now

Range indicates all the possible values that output of the function can attain .

Since we already know that the given function is an exponential ,we use the fact that an exponential term of the form a^x can not be negative . It means it can approach 0 only . It means for f(x) we say that
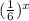`((1)/(6) )^x` can approach 0 and so f(x) approaches 0-2=-2

so the Range of the f(x) is (-2,∞)