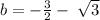ANSWER

EXPLANATION
The given equation is
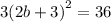
We can quickly solve this using the square root method.
We first of all divide both sides of the equation by 3 to obtain,

This implies that,
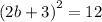
We now take the square root of both sides to obtain,
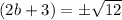
This simplifies to,
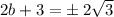
We add the additive inverse of 3, which is -3 to both sides of the equation to obtain,
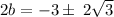
We now divide through by 2 to obtain,
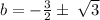
We split the plus or minus sign to obtain,
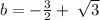
or