Answer:
42.4 cm
Explanation:
The attached diagram is the cut-section of the right conical basin.
The basin is 40 centimeters deep i.e the height of the conical basin is 40 cm.
The angle between the sloping sides is 77° i.e m∠A = 77°
As ΔABC is an isosceles triangle, so
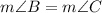
As sum of measurements of all the angles in any triangle is 180°, so
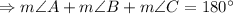
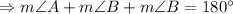
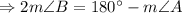
![\Rightarrow m\angle B=(1)/(2)\left[180^(\circ)-m\angle A\right]](https://img.qammunity.org/2019/formulas/mathematics/college/rvye3d42a3oefom4oa1c9yfks98agz59dp.png)
![\Rightarrow m\angle B=(1)/(2)\left[180^(\circ)-77^(\circ)]=51.5^(\circ)](https://img.qammunity.org/2019/formulas/mathematics/college/7mlvf4rwhoxton3c864txext0bj6eusudz.png)
In right angle triangle ABD,

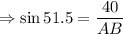
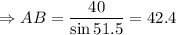 cm
cm
This is the slant height or the shortest distance between the tip of the cone and its rim.