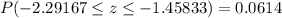Answer:
The probability that a randomly selected value will be between 660 and 680 is 0.0614
Explanation:
we are given
mean=715

standard deviation =24
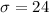
At x=660:
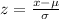
now, we can plug values

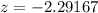
At x=680:
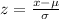
now, we can plug values
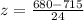
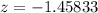
now, we can find probability
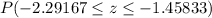
we can use table
and we get