Answer:
Refer the attached figure.
Explanation:
Given : Quadratic function
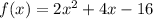
To find : The graph of the quadratic function using parabola tool?
Solution :
The given function
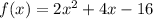
First we find the vertex form of the equation
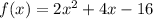
Where, a=2 ,b=4 , c=-16
Vertex is
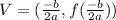
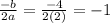
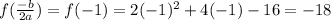
So, The vertex of the equation is (-1,-18)
Now, we find y- intercept by putting x=0 in the equation

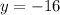
y- intercept (0,-16)
Now, we find x- intercept by putting y=0 in the equation
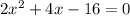
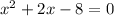
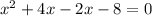

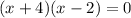

x- intercepts are (-4,0) and (2,0)
Placing all the points and plot a graph.
Refer the attached figure below.