Question

What is the abscissa of the midpoint of the line segment whose endpoints are (5, 2) and (2, 2)?

Answer 1

The abscissa of obtained mid point is 3.5

Explanation:

We are given the following information in the question:

Endpoints of a line segment are (5, 2) and (2, 2).

Mid point formula:

`(x,y) = \bigg(\displaystyle(x_1+x_2)/(2), \displaystyle(y_1+y_2)/(2)\bigg)`

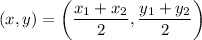
where (x,y) is the mid point and
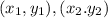`(x_1,y_1),(x_2.y_2)` are the ends of line segment.

Putting the values:

`(x,y) = \bigg(\displaystyle(5+2)/(2), \displaystyle(2+2)/(2)\bigg) = (3.5,2)`

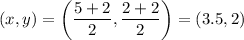
The abscissa is the x coordinate of the point.

The abscissa of obtained mid point is 3.5

Answer 2

Midpoint is (3.5, 2)

Explanation:

the midpoint of the line segment whose endpoints are (5, 2) and (2, 2)

To find midpoint of two end points we use formula

`((x_1+x_2)/(2) , (y_1+y_2)/(2))`

(5, 2) , x1 = 5 and y1= 2

(2,2), x2=2 and y2= 2

Plug in all the values and find the midpoint using the formula

`((5+2)/(2),(2+2)/(2))`

`((7)/(2),(4)/(2))`

(3.5, 2)

So midpoint is (3.5,2)