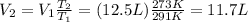We can solve the problem by using Charle's law, which states that for a transformation of an ideal gas at constant pressure, the ratio between volume and absolute temperature of the gas remains constant:
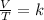
where V is the volume of the gas and T its absolute temperature.
The previous law can be rewritten as
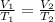
(1)
Let's convert the initial and final temperatures of the gas in Kelvin:
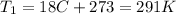
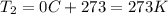
and the intiial volume is
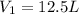
so if we re-arrange equation (1) and we use these data, we can find the final volume of the gas: