Answer:
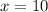
Step-by-step explanation:
We have been given an image of a triangle. We are asked to find the value of x.
We can see that triangle AFE is similar to triangle DFK. We know that corresponding sides of similar triangle are proportional, so we can set an equation to solve for x as:
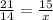
Upon cross multiplying our given equation, we will get,

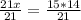
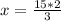
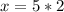
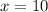
Therefore, the value of x is 10.