Question

9x^2+4y^2 = 36

The foci are located at:

a.(-√5, 0) and (√5, 0)
b.(-√13, 0) and (√13, 0)
c.(0, -√5) and (0, √5)


I already tried once, and (b) is wrong.

Answer 1

the answer is c
hope this would help you

Answer 2

c.(0, -√5) and (0, √5)

Explanation:

The equation represents an ellipse centered on origin (0,0). First, the formula is rearranged to its cannonical form:

`(x^(2))/(4) + (y^(2))/(9) = 1`

The foci are located in the lines of the semimajor axes, so, the distance between the center and any of the foci is:

`c = √(9 - 4)`

`c = √(5)`

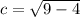
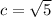
The foci are located at
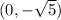`(0, -√(5))` and
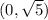`(0,√(5))`. Hence, the answer is C.