Question

What is the radius of a circle with the equation x2 + y2 – 14x + 10y = 250? A) 9 units B) 12 units C) 15 units D) 18 units

Answer 1

first, we have to change the General equation in to standard equation:

Answer 2

Option (d) is correct.

Radius of given equation is 18 units.

Explanation:

Given : The equation of circle as
`x^2+y^2-14x+10y=250`

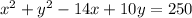
We have to find the radius of given circle.

Consider the given equation of circle
`x^2+y^2-14x+10y=250`

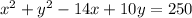
The standard equation of circle with center (h,k) and radius r is given as

`(x-h)^2+(y-k)^2=r^2`

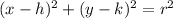
Rewriting in standard form, we have,

Grouping x and y variables, we have,

`\left(x^2-14x\right)+\left(y^2+10y\right)=250`

Convert x terms to perfect square term by adding 49 both side, we have,

`\left(x^2-14x+49\right)+\left(y^2+10y\right)=250+49`

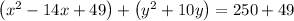
Simplify, we have,

`\left(x-7\right)^2+\left(y^2+10y\right)=250+49`

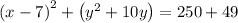
Convert y terms to perfect square term by adding 25 both side, we have,

`\left(x-7\right)^2+\left(y^2+10y+25\right)=250+49+25`

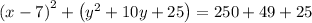
Simplify, we have,

`\left(x-7\right)^2+\left(y+5\right)^2=324`

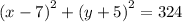
Thus, standard form is

`\left(x-7\right)^2+\left(y-\left(-5\right)\right)^2=18^2`

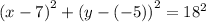
Thus, radius of given equation is 18 units.