Question

Find the length of the radius of circle C

A.
r=1
B.
r=3
C.
r=12
D.
r=15

Answer 1

Your answer would be C.) because remember always PIE-3.14 and i also did the test

Answer 2

Option D. r = 15 units

Explanation:

In this question Length of arc is given as s =
`(20)/(3)\pi`

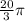
and angle inscribed at the center is θ =
`(4\pi )/(9)`

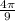
By the formula s = rθ

By placing the values of s and θ we can get the length of radius

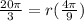
`(20\pi )/(3)=r((4\pi )/(9) )`

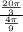
r =
`((20\pi )/(3) )/((4\pi )/(9) )`

r =
`(20\pi )/(3)* (9)/(4\pi )` = 15 unit

Therefore, Option D. r = 15 will be the answer.