Question

Q7 Q30.) Find the area of the triangle specified below.

Answer 1

When you have the side lengths of a triangle, you can use Heron's Formula to find the area of a triangle.

Heron's Formula:
`√(p(p - a)(p - b)(p - c))`
where p is half the perimeter.

Find half the perimeter: 19 + 21 + 15 = 55
55/2 = 27.5 meters

Plug the numbers in to the formula.


`√(27.5(27.5- 19)(27.5- 21)(27.5- 15))`

Now solve (I would recommend using a calculator).


`√(27.5(27.5- 19)(27.5- 21)(27.5- 15))` = 137.8
137.8 rounded to the nearest meter is 138.

A = 138 square meters

Answer 2

Heron, a mathematician gave a formula for finding the area of a triangle in terms of the three sides. The formula given by him is also known as Heron's Formula and is stated below:

If a, b, c denote the sides BC, AC and AB respectively of a triangle ABC, then
Area of triangle ABC

`= √(s(s - a)(s - b)(s - c))`where
`s = (a + b + c)/(2)`
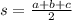
,the semi-perimeter of ∆ABC
or 2s = a + b + c

Note: This formula is useful in finding the area of a triangle when it is not possible to find the area of the triangle easily.

Now, comes to your question,

Let the sides of the triangle be a = 19 m, b = 21m and c = 15 m


`s = (a + b + c)/(2) = (19 + 21 + 15)/(2) = (55)/(2) = 27.50 \: m`

∴ Area of the triangle

`= √(s(s - a)(s - b)(s - c))`

`= √(27.50(27.50 - 19)(27.50 - 21)(27.50 - 15))`

`= √(27.50 * 8.50 * 6.50* 12.50)`

`= √(233.75 * 6.50 * 12.50)`

`= √(1519.38 * 12.50)`

`= √(18992.25)`
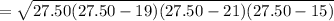
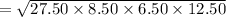
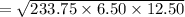
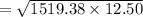
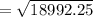
= 137.81

A => 137.81 = 138 square metres