Question

Find the point, M, that divides segment AB into a ratio of 4:7 if A is at (-33,0) and B is at (0,44)

A. (-22,-15)
B. (-22,16)
C. (-21,15)
D. (-21,16)

PLEASE ANSWER ASAP

Answer 1

D.
`(-21,16)`

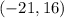
Explanation:

We have been that point, M, divides segment AB into a ratio of 4:7. Point A is at (-33,0) and B is at (0,44). We are asked to find the coordinates of point M.

We will use segment formula to solve our given problem.

When point P divides segment AB internally in the ratio m:n, then coordinates of point P can be found using formula:

`[{x=(m\cdot x_2+n\cdot x_1)/(m+n), y=(m\cdot y_2+n\cdot y_1)/(m+n)]`

Upon substituting our given values in above formula we will get,

`[{x=(4\cdot 0+7\cdot -33)/(4+7), y=(4\cdot 44+7\cdot 0)/(4+7)]`

`[{x=(0+-231)/(11), y=(176+0)/(11)]`

`[{x=(-231)/(11), y=(176)/(11)]`

`[{x=-21, y=16]`

Therefore, the coordinates of point M are
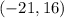`(-21,16)` and option D is the correct choice.

Answer 2

Given that M divides segment AB in the ratio 4:7, to get the point M we proceed as follows:
A(-33,0); B(0,44)
4/11[(0--33),(44-0)]
=4/11(33,44)
=(12,16)
Thus the point will be:
M=[-33+12,16+0]
M=(-21,16)

Answer: D] (-21,16)