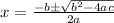Answer:
The final solution of the quadratic equation is
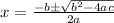
Explanation:
Given : The steps of the derivation of the quadratic formula
Step 1:
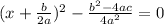
To find : Complete the steps.
Solution :
Step 1: Write the expression
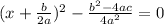
Step 2: Re-write the expression
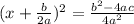
Step 3 : Square Root both side
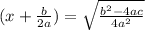
Step 4: Simplifying we get
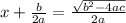
Step 5: Make x the subject
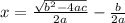
Therefore, The final solution of the quadratic equation is