Answer: The answer is

Step-by-step explanation: Given expression is
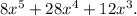
To factorise the given expression, first we need to take common the powers of 'x' which are common to all the three terms. Then, we need to factorise the remaining expression using the formula
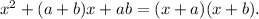
Let us start as follows
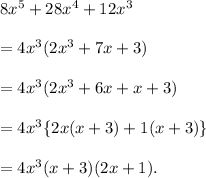
Thus, the required factorised expression is
